DEPARTMENT OF CONTROL SYSTEMS

CONTROL THEORY

NONLINEAR CONTROL SYSTEMS

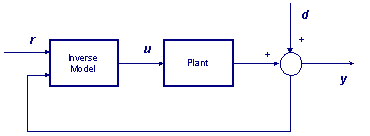
Control system design via inversion method
reduces to the construction of the inverse model

We are investigating the use of linear and difference algebraic methods for a nymber of fundamental properties of discrete-time nonlinear control system. These properties include state-space realization, controllability, observability, invertibility, transfer equivalence, and invariant structure. The properties can be further developed and applied to the design of digitally implemented feedback controllers of nonlinear systems.

ROBUST CONTROL SYSTEMS

An important practical aspect of control systems is that they should be stable despite the presence of uncertainty in the plant being controlled.

Stability region method is a useful tool for robust controller design in the case of parametric uncertainties of the plant model. The main problem is: how to approximate the stability region by some appropriate convex hull? We have focused on the use of, so-called, reflection coefficients of characteristic polynomials to generate inside and outside stability region approximations for discrete-time systems.

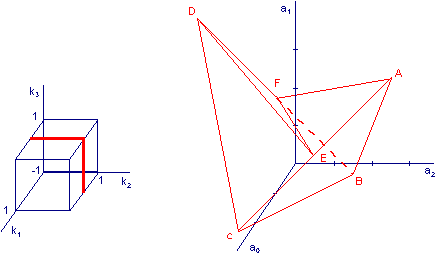
Necessary stability conditions for n = 3 ,
with reflection coefficients splitting plane k*1 = 0

STAFF

• Ülle Kotta, Ph.D.
• Ülo Nurges, Ph.D.
• Maris Tõnso, master student
• Sven Nõmm

PARTNERS IN EUROPE

• Institute de Recherche en Cybernetique de Nantes
• Sheffield University
• University of Twente