Categories are quite widely used in Theoretical Computer Science. At least, they have been necessary as an appropriate device both for describing semantics of programming languages and for expressing several important features of process algebra models. As a motivation we can point to [1] and to numerous BRICS's publications concerning this matter.
During 1996, general attributed automata (AA) of the following type were investigated:
with 
a small category, A a covariant functor from
to 
and with the to operations 
and 
given:
being a (partial) semigroup operation (changing carriers of (local) memory, and
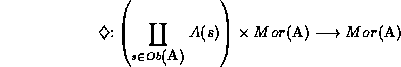
being a (partial) feedback operation ruling the processes in the whole
system - these two operations satisfying some additional
appropriate conditions.
Earlier it has been found the wreath product operation for such general AA (U.Kaljulaid, 1995). So, it has been quite essential to see what this construction gives in important for Computer Science special cases such as transition systems or Petri nets. It appears that both a single transition system and a Petri net can be considered as a category. Also, it appears that the product of transition systems (in sense of Winskel-Nielsen) important as the main source for parallel compositions of processes (see [1]) can be obtained as a subcategory in the wreath product of the labelled categories that correspond to the given systems.
Also, it is proved that for the category of usual automata with their
morphisms being monotone there exists the construction of fiber product for
decomposing such automata (U.Kaljulaid, 1996). The main difference with the
wreath product construction for such automata is that the fiber product is
indifferent with respect to the order of the components obtained. This
construction exploits properties of equality sets. These last are important
when investigating the expressibility of computations [2].
References:
1. G.Winskel, M.Nielsen. Models of Concurrency In Handbook of Logic and Foundations of Computer Science. Elsevier Sci., 1995.
2. M.Lipponen, A.Salomaa. Simple words in equality sets. Bulletin of the EATCS, No. 60, 1996, pp 123-143.